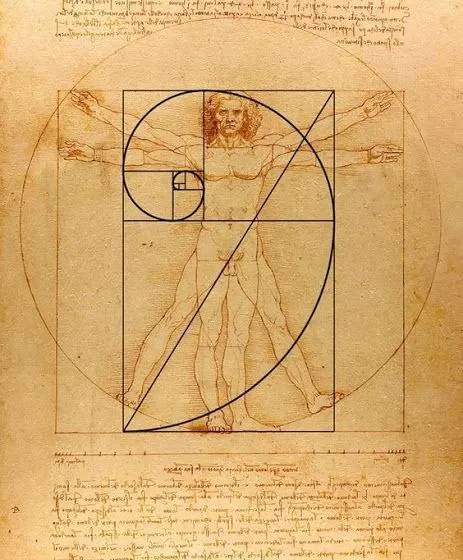
الگوریتم فیبوناچی یک دنباله عددی است که در آن هر عدد، مجموع دو عدد قبلی خود است. این دنباله به صورت زیر شروع می شود:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, …
برخی از افراد از الگوریتم فیبوناچی در بازی انفجار برای افزایش شانس برنده شدن خود استفاده می کنند.
دنباله فیبوناچی، یکی از مشهورترین و جذاب ترین دنباله های عددی در ریاضیات است. این دنباله که از اعداد 0 و 1 شروع شده و هر عدد، مجموع دو عدد قبلی خود است، به دلیل تناسبات شگفت انگیز و کاربردهای گسترده در طبیعت، علم و هنر، همواره مورد توجه دانشمندان و هنرمندان بوده است.
روش استفاده از الگوریتم فیبوناچی در بازی انفجار
بسیاری بر این باورند که بازی انفجار بر اساس الگوریتم ها و استراتژی های خاصی کار می کند و با کسب اطلاعات در مورد این الگوریتم ها می توانند ضرایب بازی را با یک دقت خیلی بهتر و بالاتر حدس بزنند. در ادامه در مورد تاثیر الگوریتم فیبوناچی بر بازی انفجار بیشتر صحبت خواهیم کرد:
- ابتدا یک مبلغ پایه (مثلاً 1000 تومان) را انتخاب کنید.
- روی ضریب 1 شرط بندی کنید.
- اگر در این دور برنده شدید، دوباره مبلغ پایه را روی ضریب 1 شرط بندی کنید.
- اگر در این دور باختید، مبلغ شرط بندی خود را در دور بعدی با استفاده از دنباله فیبوناچی افزایش دهید.
- به این ترتیب، تا زمانی که برنده شوید، به افزایش مبلغ شرط بندی خود ادامه دهید.
مزایای استفاده از الگوریتم فیبوناچی در بازی انفجار:
- این روش می تواند به شما کمک کند تا ضررهای خود را جبران کنید.
- این روش می تواند شانس شما را برای برنده شدن در بلندمدت افزایش دهد.
معایب استفاده از الگوریتم فیبوناچی در بازی انفجار:
- این روش می تواند در کوتاه مدت منجر به ضررهای سنگین شود.
- این روش هیچ تضمینی برای برنده شدن در بازی انفجار ارائه نمی دهد.
نکته:
- الگوریتم فیبوناچی فقط یک استراتژی برای بازی انفجار است و هیچ تضمینی برای برنده شدن شما در این بازی ارائه نمی دهد.
- قبل از استفاده از این روش، حتماً به طور کامل در مورد آن تحقیق کنید و از ریسک های آن آگاه باشید.
الگوریتم فیبوناچی چیست؟
الگوریتم فیبوناچی، که به دنباله فیبوناچی نیز معروف است، یک دنباله ی اعداد است که در آن هر عدد حاصل جمع دو عدد قبلی خود است.
به طور ریاضی، این دنباله به صورت زیر تعریف می شود:
Fn = Fn-1 + Fn-2, where n>1
F0 = 0
F1 = 1
در این دنباله، دو عدد اول 0 و 1 هستند و هر عدد بعدی حاصل جمع دو عدد قبلی خود است. به عنوان مثال، عدد سوم 1 + 0 = 1، عدد چهارم 1 + 1 = 2، و عدد پنجم 2 + 1 = 3 است.
این دنباله کاربردهای زیادی در ریاضیات، علوم کامپیوتر و طبیعت دارد.
برخی از کاربردهای الگوریتم فیبوناچی عبارتند از:
- محاسبه اعداد فیبوناچی: الگوریتم های مختلفی برای محاسبه اعداد فیبوناچی وجود دارد، از جمله الگوریتم بازگشتی، الگوریتم تکراری و الگوریتم ماتریسی.
- حل معادلات دیفرانسیل: الگوریتم فیبوناچی می تواند برای حل معادلات دیفرانسیل خاص، مانند معادله ی فیبوناچی، استفاده شود.
- تولید الگوهای طبیعی: الگوریتم فیبوناچی در بسیاری از الگوهای طبیعی، مانند گلبرگ های گل، شاخه های درخت و پوسته ی حلزون یافت می شود.
- ایجاد ساختارهای داده: الگوریتم فیبوناچی می تواند برای ایجاد ساختارهای داده ی کارآمد، مانند توده های فیبوناچی، استفاده شود.
- تحلیل مالی: الگوریتم فیبوناچی در تحلیل مالی برای شناسایی سطوح حمایت و مقاومت در نمودارهای قیمت استفاده می شود.
رمزگشایی از راز دنباله فیبوناچی
- فرمول دنباله:
F(n) = { 0 if n = 0
1 if n = 1
F(n – 1) + F(n – 2) if n > 1 }
- ویژگی های کلیدی:
- هر عدد، مجموع دو عدد قبلی خود است.
- نسبت دو عدد متوالی به عدد طلایی (1.618) نزدیک می شود.
- در طبیعت، در ساختار گیاهان، جانوران و حتی کهکشان ها یافت می شود.
- در علم کامپیوتر، رمزنگاری، الگوریتم های جستجو و مرتب سازی و فشرده سازی داده ها کاربرد دارد.
- در هنر، در نقاشی، مجسمه سازی و موسیقی به کار می رود.
کاربردهای شگفت انگیز:
- طبیعت:
- در گلبرگ های گل، آرایش برگ ها روی ساقه، و ساختار مخروط کاج
- در پوسته حلزون و تناسبات بدن انسان
- علم:
- در مدل سازی رشد گیاهان، الگوهای آب و هوایی و توالی یابی DNA
- در نظریه اعداد، فیزیک و هندسه
- هنر:
- در نقاشی های داوینچی، مجسمه های میکل آنژ و معماری یونان باستان
- در موسیقی باخ، موتزارت و آهنگسازی مدرن
- کامپیوتر:
- در الگوریتم های جستجوی سریع، فشرده سازی تصاویر و رمزنگاری اطلاعات
- در هوش مصنوعی و یادگیری ماشین
رمز و راز عدد طلایی
- نسبت طلایی (1.618):
- حاصل تقسیم هر عدد فیبوناچی به عدد قبلی خود، به عدد طلایی نزدیک می شود.
- این عدد در طبیعت، علم و هنر به عنوان یک تناسب ایده آل و زیبا شناخته می شود.
- در معماری، نقاشی، مجسمه سازی و طراحی گرافیک کاربرد دارد.
چالش ها و فرصت ها:
- محاسبه اعداد بزرگ:
- محاسبه اعداد بزرگ فیبوناچی با روش های سنتی دشوار است.
- الگوریتم های جدیدی برای محاسبه سریع و دقیق این اعداد ارائه شده است.
- کاربردهای نوین:
- دانشمندان به دنبال کاربردهای جدیدی برای دنباله فیبوناچی در زمینه های مختلف هستند.
- هوش مصنوعی و یادگیری ماشین، فرصت های جدیدی برای استفاده از این دنباله در حل مسائل پیچیده ارائه می دهد.
دنباله فیبوناچی، یک راز شگفت انگیز در دنیای ریاضیات است که رمزگشایی از آن، دریچه ای به سوی دنیای علم، طبیعت و هنر می گشاید. تناسبات و کاربردهای گسترده این دنباله، آن را به ابزاری قدرتمند در دستان دانشمندان، هنرمندان و برنامه نویسان تبدیل کرده است.